Простота й точність: як спрогнозувати LTV для ігор, якщо ви не Data Scientist
Хен Карні, Data Science Director у Plarium Herzliya
Оригінал статті на англійській мові
Прогноз життєвого циклу клієнта (LTV) – це один із найважливіших показників, які потрібні менеджерам компаній із різних сфер діяльності. Зазвичай LTV є оцінюванням сукупного очікуваного доходу від одного клієнта за весь час його взаємодії з продуктом чи послугою. Розрахунок LTV здебільшого використовується для вимірювання прибутковості продукту в довгостроковій перспективі та визначення того, які методи маркетингу та продажів дають максимальні результати.
Є чимало способів розрахунку цього показника для продукту, зокрема для ігрового: від розгляду сегментів гравців, тобто сукупності їхніх головних ознак (географія, платформа, джерело залучення тощо) до розрахунку такого показника для кожного окремого гравця. Вибраний спосіб також впливає на рівень складності й точності прогнозу. З погляду сегментів можна виконати математичне обчислення й отримати показник, який відповідає середньому доходу від середньостатистичного гравця в цьому сегменті. Якщо брати ігри з механізмами монетизації, то необхідно помножити середній платіж на кількість платежів, які гравець здійснить за весь час до його вибуття з гри (для детальнішої інформації ознайомтеся з моделлю «Buy Till You Die», яка була розроблена в 1987 р.).
На рівні одного гравця розрахунок LTV переважно означає прогнозування за допомогою машинного навчання. Тобто потрібно брати до уваги різні чинники гравця, зокрема головні ознаки сегмента, але водночас фокусуватися на поведінці гравця в грі та знаходити тенденції, які можуть дати уяву про майбутній дохід.
Безперечно, прогнозування за допомогою машинного навчання – це значно точніший метод, ніж будь-який високорівневий розрахунок. Воно дає змогу розрізняти типи гравців та визначати тенденції в їхній манері гри, які потім можна використовувати для оцінювання інших аспектів. Можна встановити, як довго користувачі гратимуть у гру, як добре вони її зрозуміють, скільки часу та зусиль вони витратять на накопичення своїх внутрішньоігрових ресурсів, а також як нові версії, функціональності та ігрові пакети вплинуть на все вищезазначене. Однак такі моделі потребують занадто багато часу для розроблення (величезний об’єм даних і потужне обладнання для їх оброблення) і, авжеж, спеціаліста, який знає, як об’єднати всі ці дані в прогноз.
Тому, залежно від завдання та наявних ресурсів, кожний розробник ігор має визначитися, наскільки розрахунок LTV відповідає його потребам, а також скільки часу та зусиль він готовий вкласти в нього. На щастя, у багатьох випадках достатньо звичайного високорівневого розрахунку. Якщо виконати його правильно, він буде досить точним – припустима похибка не перевищуватиме 10 %.
У цій статті хотілося би зупинитися на високорівневому посегментному розрахунку LTV, який порівняно легко виконати, наприклад, за допомогою логарифмічної регресії.
Що потрібно для розрахунку LTV у сегменті?
Життєвий цикл. Треба визначити час, який гравець проведе в грі, а для цього потрібно зрозуміти його активність і об’єктивний термін, під час якого будуть здійснюватися платежі до вибуття гравця. Умовно назвімо це «життєвим циклом» гравця. Залежно від гри, він може складати тиждень, місяць або навіть декілька років.
Чим довше цей період, тим складніше прогнозувати майбутнє, адже протягом тривалого часу можуть змінюватися різні зовнішні та внутрішні змінні. Зовнішніми змінними можуть бути переломні події в житті (через які гравець втрачає цікавість до гри), глобальні події (наприклад війна, стихійні лиха, епідемії), професійні та економічні зміни (перехід на іншу роботу або економічна криза). Внутрішні змінні простіше контролювати, тому що вони стосуються лише гри: сюди можна віднести додаткові частини, зміни у внутрішньоігрових механізмах і подіях, нову функціональність і пакети, що можна придбати.
Отже, потрібно сфокусуватися на проміжку часу, який краще покаже дохід, точніше, більшу частину доходу. На якому етапі розробник одержить приблизно 85 % доходу? Саме це необхідно з’ясувати.
Дані. У наявності мають бути статистичні дані щонайменше за декілька місяців. Їхня гранулярність залежить від певного проміжку часу. Тобто на основі яких даних потрібно виконувати розрахунок: щоденних, щотижневих або щомісячних? Чим більше є релевантних даних, тим глибше має бути гранулярність.
Якщо ви маєте дані за 5–6 місяців і більше, щотижневої або щомісячної гранулярності буде достатньо (залежно від мінливості внесків гравця). Якщо є дані за менший період, краще вибрати щоденну або щотижневу гранулярність.
Що таке релевантні дані? Це дані, які належать до поточної версії або пропозиції продукту. Якщо у функціональностях, ігрових пакетах (підписка, контент, ціна) або зовнішньому вигляді гри відбулися суттєві зміни, дані можуть бути менш показовими, що зменшить точність розрахунку.
Розуміння регресії. Регресія – це математична залежність між групами параметрів або змінних, яка дає змогу використовувати наявні дані для оцінювання даних, яких бракує.
У нашому випадку ми беремо поточний дохід у сегменті гравців і намагаємося оцінити розмір майбутнього доходу. Це можна виконати кількома способами: переважно використовується метод змінного середнього значення або лінійна регресія. В ігровій індустрії краще спиратися на логарифмічну регресію, коли йдеться про прогнозування на 5–6 місяців.
Взаємозв’язок між доходами приймається з огляду на логарифмічне рівняння, яке виглядає десь так:
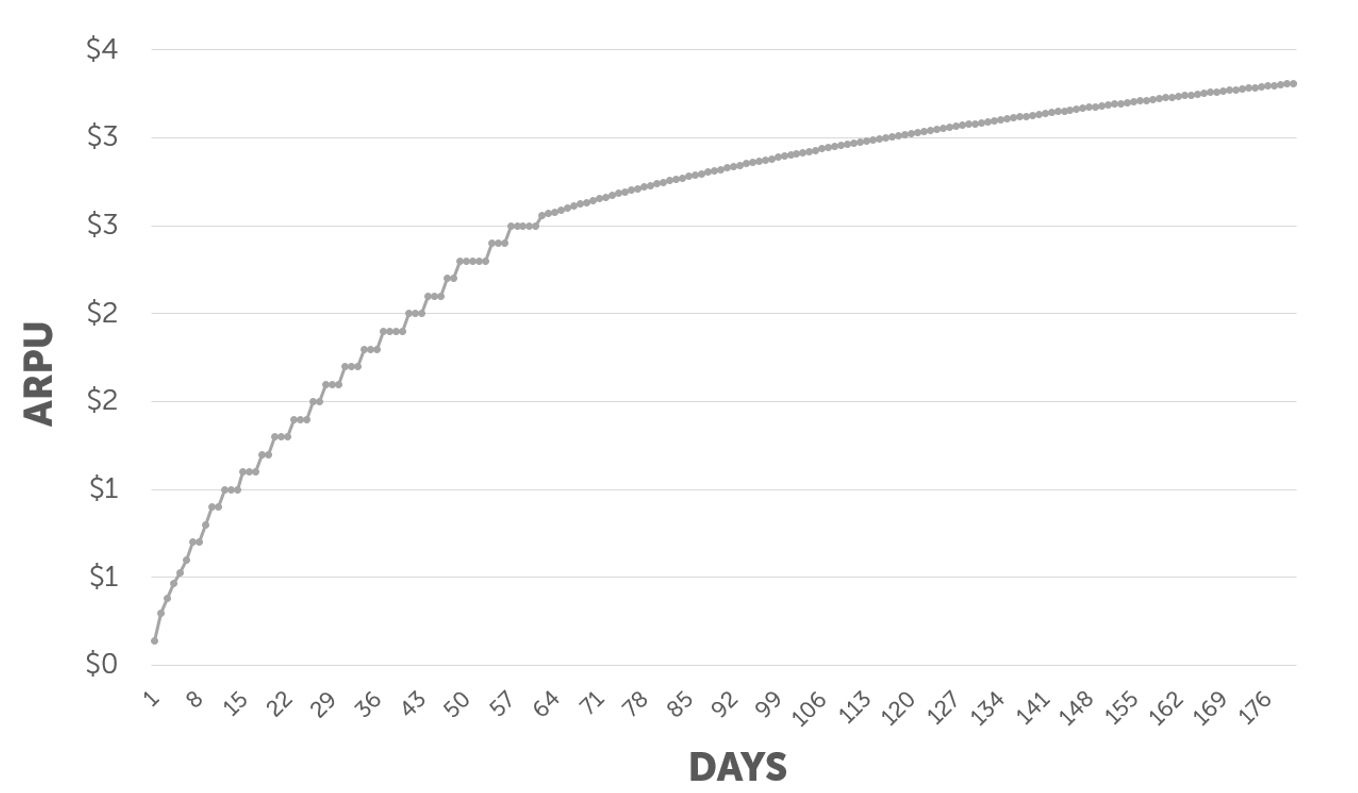
Графік, який показує прогноз LTV на 180 днів з огляду на перші 60 днів
Хоча перші 60 днів ARPU (середній дохід на користувача) основані на реальних даних, інші 120 днів основані на натуральному логарифмічному рівнянні ln(x), яке отримано на основі реальних даних.
Порядок розрахунку
Перший етап. Необхідно взяти дані, на основі яких буде виконуватися обчислення. Це може бути ARPU або ROAS (окупність витрат на рекламу). Потім треба вибрати гранулярність розрахунку (щоденна/щотижнева/щомісячна) і розділити її по когортах. Якщо брати 3 місяці щоденних даних, то в підсумку отримаємо 90 стовпців ARPU (D0 ARPU, D1 ARPU,…, D90 ARPU) і 90 рядків (за кожний день).
Наведемо приклад щоденних даних про ARPU:
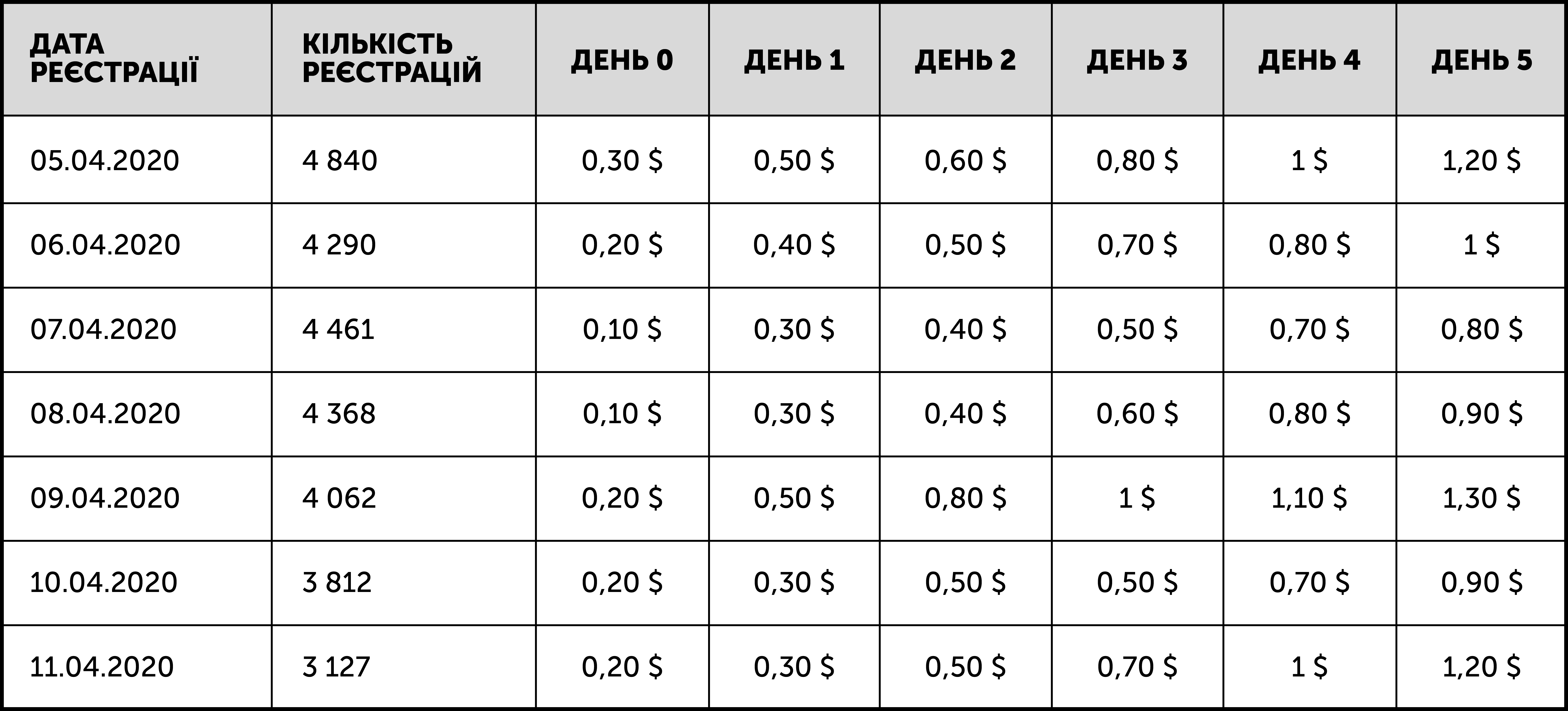
Другий етап. Треба обчислити середнє зважене значення, тобто середній показник ARPU за кожний день. У такий спосіб ми отримаємо результат за перші дні. Згодом приріст значення за кожний день зменшуватиметься під час проходження когорти.

Третій етап. Потрібно видалити 3–5 верхніх та 3–5 нижніх дати з максимальними та мінімальними значеннями. У такий спосіб ми вилучимо 5 % верхніх і 5 % нижніх випадних показників, які можуть спотворити середню тенденцію.
Четвертий етап. Виконаймо розрахунок за логарифмічним рівнянням із певними днями з наших даних. Це можна зробити за допомогою Excel, R, Python (особливо підійдуть інструменти matplotlib.pyplot і scipy.optimize curve_fit) або іншої програми статистичного аналізу (наприклад, SPSS або MATLAB) залежно від ваших уподобань.
Незалежно від вибраного способу, регресія передбачає таку формулу:
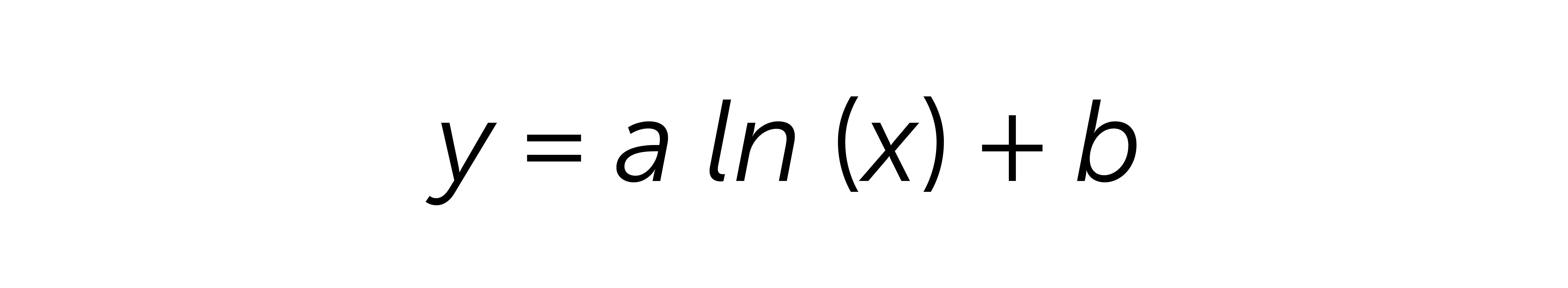
де:
x– кількість днів, наприкладx = 3для 3-го дня ARPU;
y– підсумковий ARPU за певний день x, наприклад результат рівняння за 61-й день.
Зважаючи на дані вище, була отримана така логарифмічна формула:
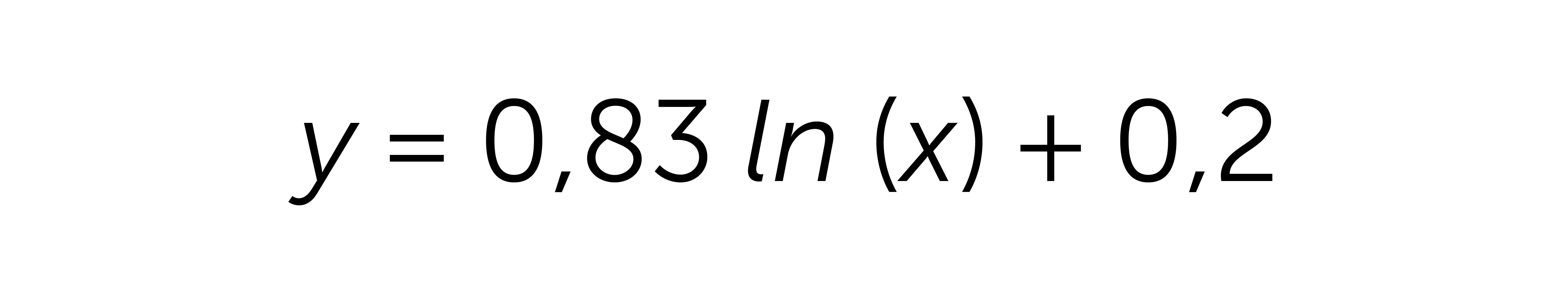
Отже, вищенаведену формулу можна застосовувати для прогнозування ARPU за 60+ днів. Ми використовуватимемо обчислене середнє значення за перші 60 днів як реальні дані, а потім візьмемо наступні дні, приймаючи x за відповідний день.
Іноді формула потребуватиме ручного коригування. Одним із параметрів, що коригуються, може бути відрізок осі y (параметр b у рівнянні вище), щоби підняти або опустити криву рівняння для більшої відповідності кривій реальних даних. Ще одним параметром може бути момент часу, коли зростання доходу починає знижуватися. Якщо такий момент відбувається пізніше, ніж обраний відрізок часу реальних даних (у прикладі вище це 60 днів), можна додати іншу формулу, яка дасть змогу ліпше прогнозувати дохід (наприклад, лінійну регресію).
Залишається тільки пограти з даними, розділити їх на сегменти, знайти відмінності та порівняти дані з ціною за встановлення (CPI), щоби визначити прибутковість гри.
Рекомендується періодично повторювати цей розрахунок і спостерігати, як змінюється прибутковість гри, що дасть уяву про те, коли залучення гравців може бути недоцільним.
Наразі спробуйте виконати розрахунки самостійно!



